“Deep”合成関数
“Deep”合成関数
コンピュータないし、ソフトウェアを抽象的にとらえると関数の集合体と考えることができます。
入力データのパターンが限定的であれば、プログラマがその限定的なパターンに応じた関数をプログラムしてあげればよいのですが、例えば、画像や音声、自然言語を入力データとしてとらえて、それらに対応した処理をしなければならない場合、そのプログラムを作成するのも現実的ではないし、膨大なデータに適切に処理できるようなプログラムは処理速度の問題を抱える可能性が極めて高くなります。
ディープラーニングによって作り出す関数は膨大な入出力のデータパターンから、そのような入出力の結果を返すような近似関数を算出する形で作り出されます。
画像であっても、音声であっても、文字列であってもこれらのデータは数字を使って表現することができます。
入力データを $\vec x = (x_0, x_1, \cdots, x_{m-1})$
出力データを $\vec y = (y_0, y_1, \cdots, y_{n-1})$
とすると
$$
\vec y = f(\vec x)
$$
$$
\begin{pmatrix}
y_0\\
\vdots\\
y_{n-1}\\
\end{pmatrix}
=
\begin{pmatrix}
f_0(x_0,\cdots,x_{m-1})\\
\vdots\\
f_{n-1}(x_0,\cdots,x_{m-1})\\
\end{pmatrix}
$$
と数式を使って表現できます。
各$f_i$は$n$変数,1値関数となります。
$f_i$の近似関数として、最もシンプルな関数は
$$
y_i = a_{i0}x_0 + a_{i1}x_1 + \cdots + a_{im-1}x_{m-1} + b
$$
という形の線形1次関数となります。
この場合、$m+1$個のパラメータを調整して、近似関数を求めるわけですが、これではどのようにパラーメータを調整したとして、様々なバリエーションの入出力データパターンに近似する関数になることは、ほぼありえないといってもよいと思います。
次数を上げることで、表現力は上がります。
例えばn変数、2次関数ならばどうでしょうか。
$$ y_i = a_{i00}x_0^2 + a_{i01}x_0 x_1 + \cdots + a_{i0m-1}x_0 x_{m-1}\\ + a_{i11}x_1^2 + a_{i12}x_1 x_2 + \cdots + a_{i1m-1}x_1 x_{m-1}\\ \vdots + a_{im-1m-1}x_{m-1}^2\\ + a_{i0}x_0 + a_{i1}x_1 + \cdots + a_{im-1}x_{m-1} + b $$
この場合の関数を決定するためのパラメータ(係数)の数は $$ _{m+1} C_2 + m + 1 $$ となります。
中学生でならった2次関数(1変数)を思い出していただければ、これでもまだ表現力は貧弱と言わざるを得ません。
一般に、次数を増やすほど、表現力が上がるわけですが、例えば$l$次、$m$変数、$n$値関数のパラメータ(係数)は
となり、特に変数$m$,次数$l$の増加に対して、関数を決定付けるためのパラメータが爆発的に増えることがわかります。(重複有り組み合わせの場合の数)
この問題を解決するための手法が「関数を合成する」という手法です。
例えば、100変数、100値、1024次の関数の項の数すなわちパラメータの数は、
になります。
しかし、これを100変数、100値、2次の関数を10回合成することによって、100変数、100値、1024次の関数を作ると必要なパラメータの数は
と圧倒的に少ないパラメータで同じ次数の関数を表現することが可能になります。
それぞれの関数を模式図で描くと以下のようになります。
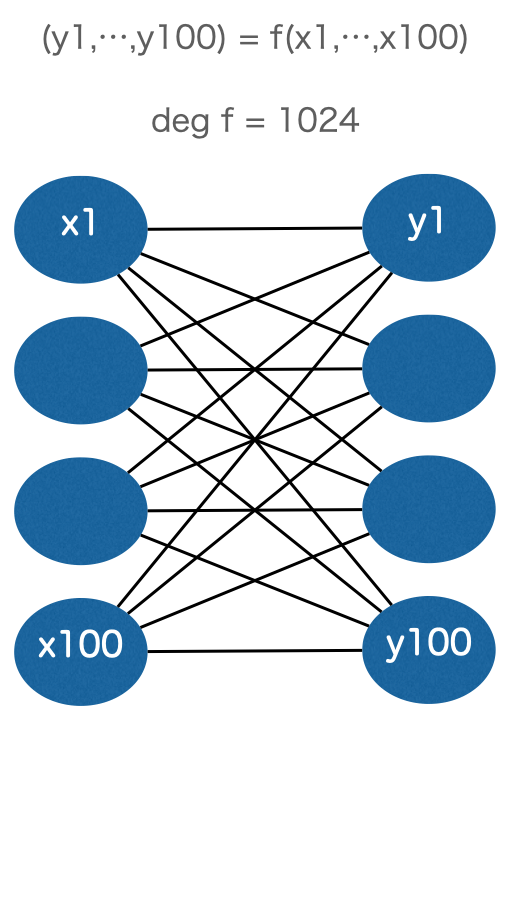
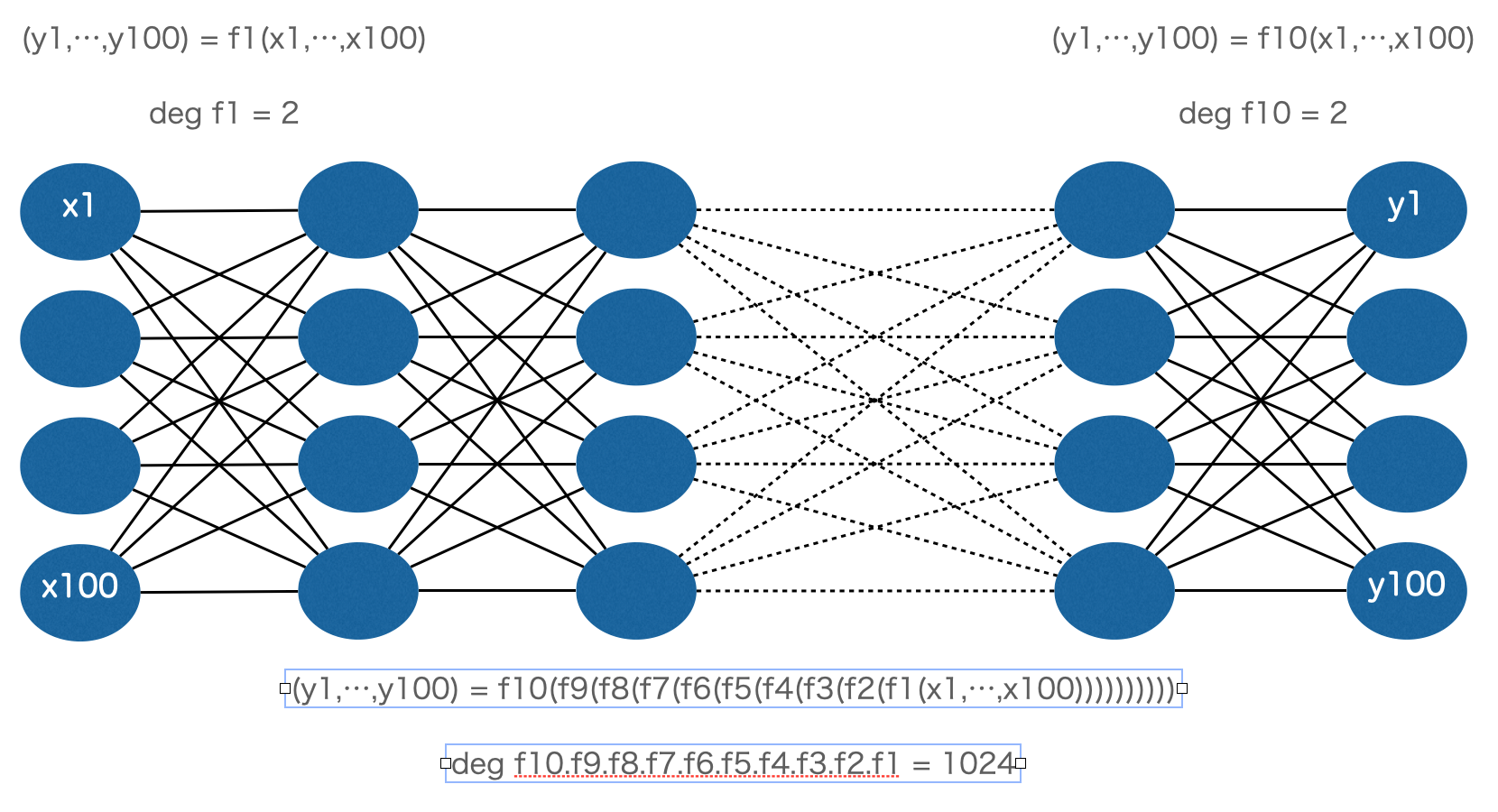
この“深い”スタックの関数呼び出しにより、大量データから精度の高い近似関数を作る仕組みが“Deep”Learning の名前の所以とされています。
(※この例では、中間層に現れる関数すべてを100変数、100値関数としましたが、この中間層のファイルの次元は変えることも可能です。)
実際に使われる関数は多項式ではありません。微分のしやすさ等を考慮して以下のような関数を合成して作ることになります。