Convolutional Neural Network
Convolutional 層
例えば、1000x1000のフルカラー(RGB=255,255,255)の画像データを入力データにして、この画像を10種類のラベルに分類分けをするために全結合層(隠れ層は100個のニューロンを1層)を構築した場合、パラメータの数はいくつになるでしょうか。
この数をPとするとそれは
3千億個のパラーメータが必要になります。
このニューラルネットワークに大量の教師データを読み込ませて、勾配降下法を用いてパラメータを収束させるのには、途方も無い時間が必要になってしまいます。
この問題を解決するのがCNNです。
一言でいえば、CNN Convolutional Neural Networkは"特徴量"を抽出するための、多次元関数です。
特徴を抽出するための比較的次元の低いベクトルを設定し、与えられた多次元データに対して、次元をずらしながら、内積をかけていきます。
特徴ベクトルと一致する部分があると、その内積値は大きくなります。
このようにして高次元のデータから特徴を抽出することを可能にします。
例えば、数字を判定するNeural Network関数を作りたいとします。
様々な大きさの画像が与えられたとして、それを人が見て数字を判定する場合、まず数字の位置を特定して、その中にそれぞれの数字のもつ特徴が含まれているかどうかを判定するはずです。
以下の例をみれば、比較的容易にCNNを理解できるのではないでしょうか。
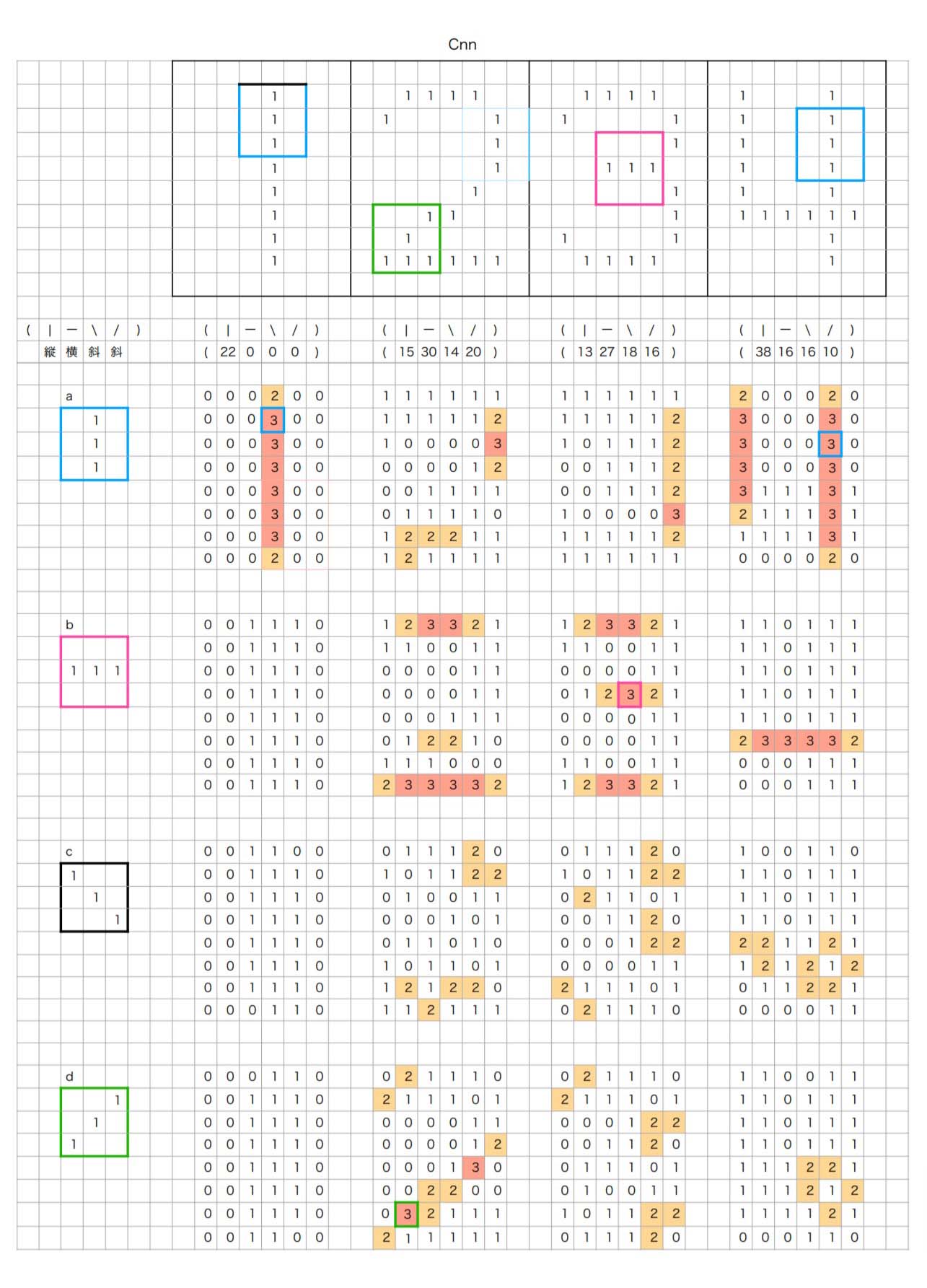
この例では 8x10 の画像データに対して、3x3で"縦","横","右斜下","右斜上"という4つの特徴ベクトルを定義して、それぞれの画像に対して、1ピクセルづつずらしながら内積を計算していっています。
内積の数字が"1"となっているものは、特徴ベクトルと1点のみが重なっているということであり、これは線分の特徴を表しているとわいえないので、内積の値が"2"以上のものをそれぞれの画像毎に足し合わせて、各数字の特徴量とします。
この例では、元画像があまりに解像度が低く(8x10)、かつ色調もブール値でしか表現されていないため、かなり荒い精度の特徴抽出になってしまっていますが、少なくとも、
- "1"は中央付近に縦成分が多く、横、斜め成分が皆無
- "2"は右上に縦成分があり、上下に横成分があり、右上から左下への斜め成分がある
- "3"は右端に眺めの縦成分があり、上下中央に横成分があり、斜め成分も全体的に散らばっている
- "4"は左右に強めの縦成分があり、ややしたに横成分がある という感じで、それぞれの数字の特徴抽出ができていることが見て取れると思います。
これら縦、横、右斜、左斜という4つの合計値を出すだけでも、数字の特定が可能であることが想像できると思います。
元画像、8x10=80次元のベクトルを4次元のベクトルとして表現することを可能にしており、CNNが画像のような極めて高い次元の無味乾燥なビットデータの配列から、意味のあるより少ない次元の特徴量を抽出することを可能にします。
Pooling 層
「Convolutional Neural
Network」では、画像のような極めて高い次元のデータから特徴量を抽出するのに活躍をするという話をしました。
多くの場合Convolutional
Neural Networkでは、Convolution層とともにPooling層が同時に使われます。
Pooling層は、ニューラルネットワーク関数に"パラメータ削減"と”柔軟性の増加”という効果をもたらします。 Convolutional Neural
Networkでも使用した例を見ながら説明したいと思います。
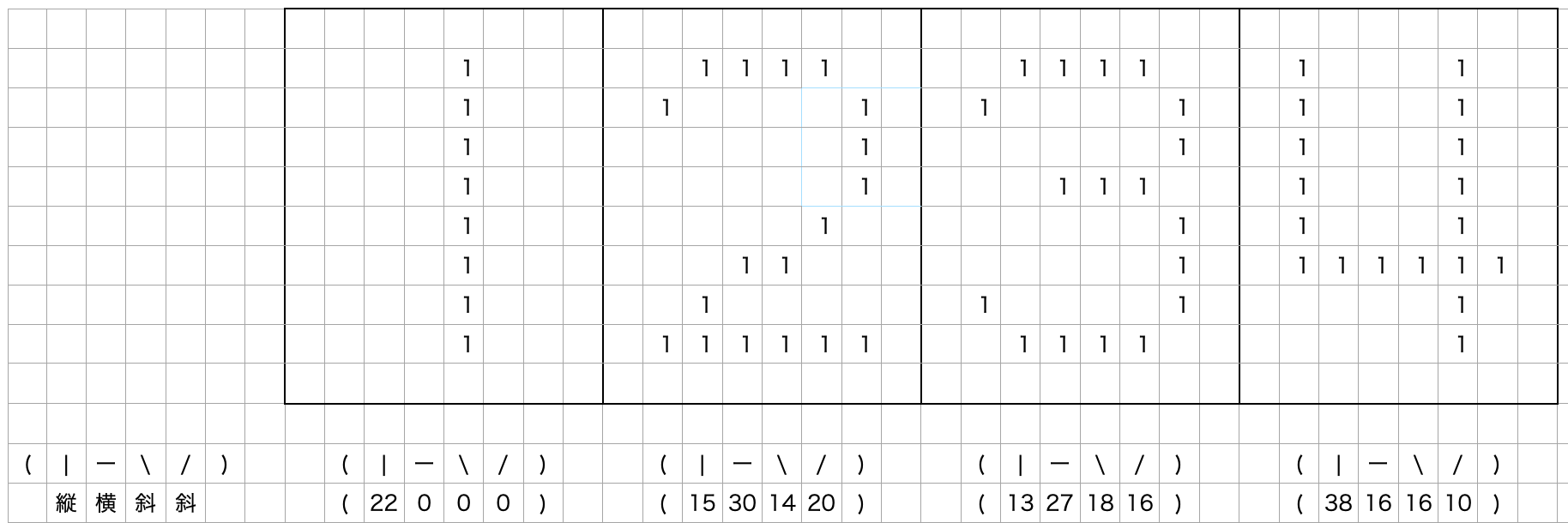
この例では、8x10=80次元のデータを縦、横、右斜、左斜の特徴量に変換し、4次元のデータで1,2,3,4という数字を表現していました。
これだけの情報でもこの4つの数字を判別することはできるかもしれませんが、この手法はかなり”雑”と言わざるを得ません。この手法では、縦、横等の各特徴量の出現する位置についての情報を全て失ってしまってしまいます。
では、特徴が出現する位置すべての情報をもてばよいかといえば、そうでもありません。
例えば、この画像は"2"の横成分の出現箇所を正確に反映したものですが、
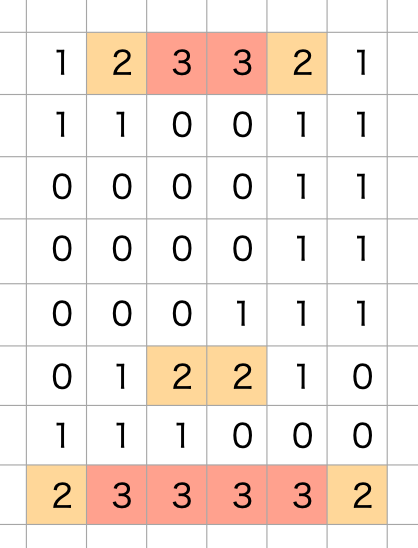
たとえ、この位置が前後左右に多少ずれていたとしても、"2"の横成分が出現する位置としては、妥当であり、完全にこの位置にこの横成分が出現しないと"2"の横成分として認めないというのでは、あまりに柔軟性がありません。人がより柔軟に判断ができるようのと同じようにコンピュータにも柔軟性をもたせたいと思えば、この全ての情報をもつということも数字を判断する上で弊害になりかねません。
そこで、プーリング層という層が必要になります。
話をわかりやすくするために、1つの画像を縦2つ、横2つに区切り合計4つのエリアでの特徴量の和を考えます。
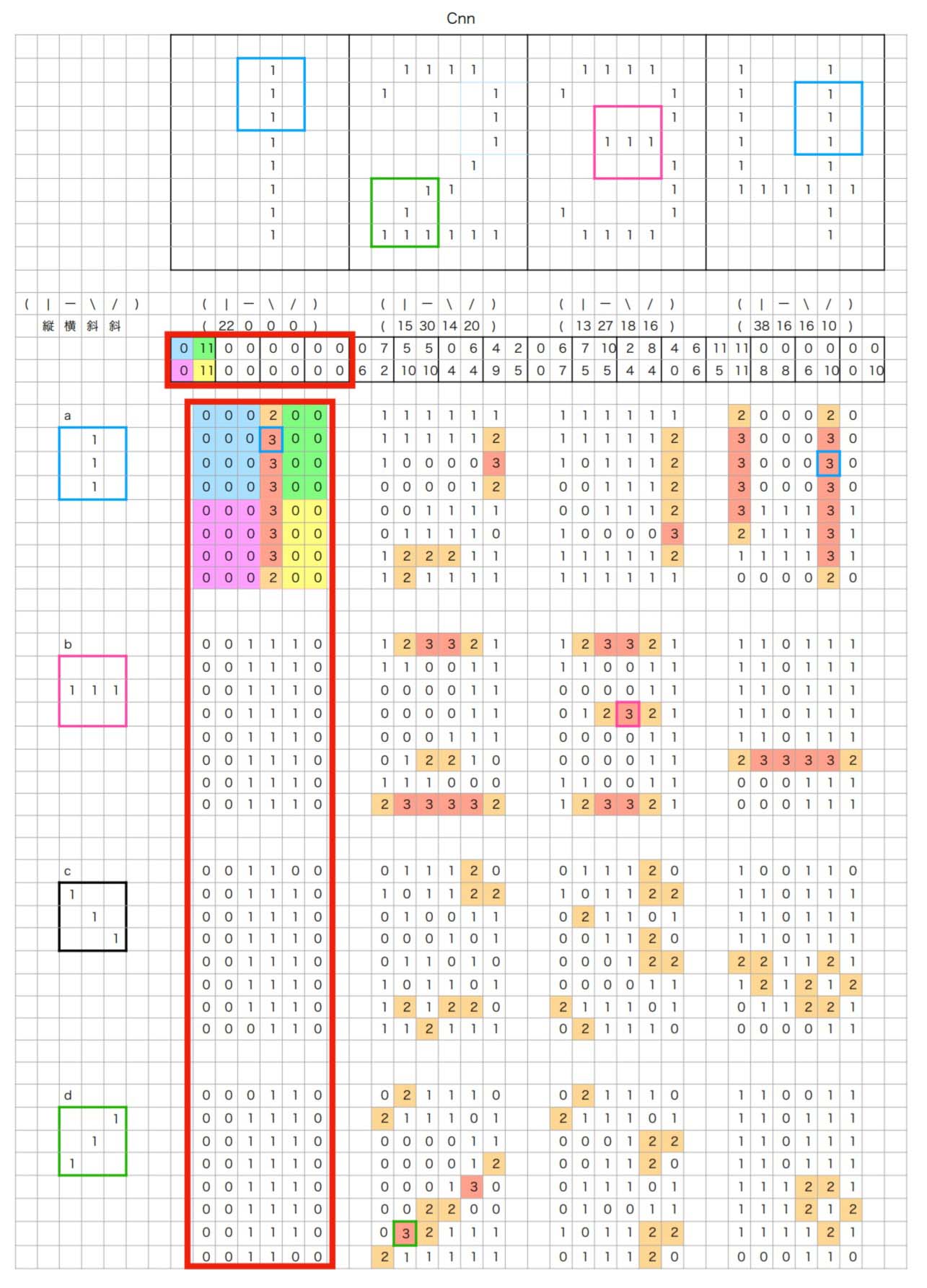
こうすることで、1つの画像データを4つのエリア、4つの特徴量、合計16次元のベクトルで表現できます。
4次元のベクトルよりはパラメータが多くなってしまいますが、80次元よりは圧倒的に少なく、しかも、特徴量の"おおよその"位置情報も含んでいます。
この"おおよそ"という部分がとても重要であり、本来コンピュータが不得意としてきた分野です。
あえて8x10というエリアではなく、2x2というエリアにわけることで、特徴量の位置が多少ずれたとしても、広いエリアの総和を考えていることにより、このズレを吸収してくれる役割を持ってくれるのです。
(※多くの場合は"Max Pooling"といって、そのエリアの最大値を採用するというやり方をしますが、この画像の例では、画像およびConvolution層の取り方ともに粗いため、各ドットの特徴量が2もしくは3の2つの値しか取りえないので、総和によるPooling層を採用しています。)
このように、CNNでは、Convolutional層とPooling層を繰り返しながら、
- 数百万次元の
- 無味乾燥で、
- 柔軟性のない
ベクトルデータから
- より少ない次元の
- 意味のある
- 柔軟性のある
データに変換していきます。
このようにして得られた多次元データを全結合層につなぐことで、人と同じレベルの精度でコンピュータが画像を認識することが可能になるのです。